Overview: The concept of Time Value of Money (TVM) is a foundational principle in financial mathematics and actuarial science. It asserts that money available today is worth more than the same amount in the future due to its potential earning capacity. This concept is vital in the actuarial field, particularly for pricing insurance products, determining premiums, evaluating investments, and managing the financial risks associated with long-term liabilities. Understanding TVM is crucial for actuaries working in reinsurance companies like GIC Re, as it helps in assessing the present value of future liabilities, pricing policies, and calculating reserves.

Key Concepts in Time Value of Money:

1. Definition of Time Value of Money:

   • The core principle of TVM is that a dollar today is worth more than a dollar in the future because of its potential to earn returns or accrue interest. In other words, the value of money changes over time due to inflation, interest rates, and opportunity cost.

2. The Components of TVM:

   • Present Value (PV): The value today of a sum of money that is to be received or paid in the future. It reflects how much a future payment is worth in today’s terms.
   • Future Value (FV): The value of a sum of money at a future point in time, considering its earning capacity. It helps determine how much a current investment will grow over a specified time period at a given rate.
   • Interest Rate (r): The rate at which money grows over time. This could be a simple interest rate or a compounded rate.
   • Time (n): The number of time periods (e.g., years, months) over which the money will grow or be discounted.

3. The TVM Formulas:

   • Present Value (PV):
     ​
     • Where:
       • PV = Present Value
       • FV = Future Value
       • r = Interest rate per period (expressed as a decimal)
       • n = Number of periods (years, months, etc.)
   • Future Value (FV):
     
     Where:
     • • FV = Future Value
       • PV = Present Value
       • $r$ = Interest rate per period
       • $n$ = Number of periods

4. Simple Interest vs. Compound Interest:

   • Simple Interest: Interest is calculated only on the principal amount.
     
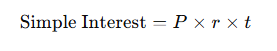
      Where:
     • P = Principal amount
     • $r$ = Interest rate
     • t = Time period
   • Compound Interest: Interest is calculated on both the principal amount and the accumulated interest from previous periods.
     
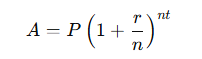
      Where:
     • $A$ = Amount (principal + interest)
     • $P$ = Principal
     • r= Annual interest rate (decimal)
     • n = Number of compounding periods per year
     • t = Time in years

5. Application of TVM in Actuarial Science:

   • Actuaries use TVM to assess future liabilities and determine the appropriate reserves for insurance companies. By applying the concept of present and future value, actuaries can calculate premiums, annuities, pensions, and other financial instruments.
   • Discounting: The process of determining the present value of future cash flows. In the insurance and reinsurance industry, this technique helps in assessing the financial viability of a product over time.
   • Annuities: TVM is also essential when evaluating annuities, where payments are made regularly over time. Actuaries use formulas to determine the present and future values of these payments.

Example:

Imagine an insurance company needs to calculate the present value of a claim payment of ₹1,00,000 that is due in 5 years. The interest rate is 8% annually. Using the present value formula:

Thus, the present value of ₹1,00,000 due in 5 years at an interest rate of 8% is approximately ₹68,069.

Applications of TVM in GIC Re:

1. Pricing Reinsurance Contracts:

   • TVM helps actuarial teams determine the appropriate pricing for reinsurance contracts by considering future payouts and the risk associated with them.

2. Estimating Claims Reserves:

   • Actuaries calculate reserves by discounting future claim payments to the present, ensuring the insurer maintains sufficient funds to meet its obligations.

3. Investment Decisions:

   • TVM is used in evaluating the profitability of investment opportunities by considering the time value of cash flows, helping the company make informed decisions about where to allocate funds.

4. Premium Calculations:

   • TVM is essential for determining how much premium should be charged today to cover the future liabilities and potential claims.

Conclusion:

Understanding the time value of money is essential for actuaries, especially in the context of reinsurance, where future obligations and their associated risks must be quantified and managed. By mastering TVM concepts, actuaries can make better financial decisions, optimize premium pricing, and ensure that insurance companies remain financially stable in the long term.