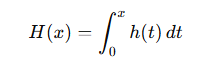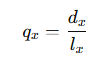Introduction

Survival models and life tables form the foundation of actuarial science, particularly in life insurance and pension planning. These tools help actuaries estimate the likelihood of survival or death at various ages, making them essential for assessing risks, calculating premiums, and designing products.

Survival Models

Definition:

A survival model predicts the probability of survival over time for individuals or populations. It is mathematically expressed as a function of time, accounting for mortality rates, life expectancy, and other factors.

Key Terms:

1. Survival Function S(x):
   Represents the probability that a person of age $x$ survives to at least age $t$:

   

   where T is the random variable representing the time of death.

2. Hazard Function h(x):
   The instantaneous rate of failure (death) at a specific age, given survival to that age:

   ​

   where f(x) is the probability density function.

3. Cumulative Hazard Function H(x):
   Summarizes the accumulated risk over time:

   

4. Force of Mortality μ(x):
   The hazard rate at a specific age in the context of continuous-time survival analysis.

Life Tables

Definition:

A life table is a statistical table that summarizes the mortality experience of a population. It provides probabilities of death, survival, and related measures for each age.

Structure of a Life Table:

1. $x$: Age.
2. lx: Number of individuals alive at age $x$.
3. dx​: Number of deaths between ages $x$ and x+1
4. qx: Probability of death between ages $x$ and x+1
   ​​
5. px​: Probability of surviving from age $x$ to age x+1
   ​
6. Tx​: Total future years lived by all individuals at age $x$.
7. ex: Life expectancy at age x
   
   

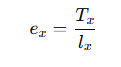
Applications in Actuarial Science

1. Life Insurance:
   Survival models and life tables help calculate premiums and reserves for policies by estimating mortality risks.

2. Pension Plans:
   They are used to determine annuity payments and assess the sustainability of pension funds.

3. Healthcare Analysis:
   Useful in estimating survival rates for patients and evaluating medical interventions.

4. Risk Management:
   Helps identify and quantify longevity risk for insurers and pension funds.

Mathematical Example

Life Table Calculation:

If l40=10,000 and d40=500, calculate q40and p40

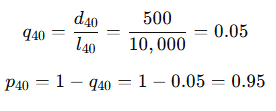
This means a 40-year-old has a 5% probability of dying before age 41 and a 95% probability of surviving.

Case Study: Application in Reinsurance

In a reinsurance context, survival models and life tables are used to price products like group term life insurance. For instance, a reinsurer may calculate the probability of multiple claims in a portfolio based on survival probabilities from life tables.

Engagement Exercises

1. Use a simple life table to calculate the survival probabilities for ages 30 to 40.
2. Derive the force of mortality (μ(x)) for a given hazard function.