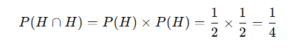Introduction to Probability Theory

Probability theory is the mathematical study of uncertainty. It provides a framework for quantifying and understanding random phenomena, making it a cornerstone of actuarial science. Actuaries rely on probability to evaluate risks, set premiums, and predict future events.

Key Definitions and Concepts

1. Experiment

   • A process or action leading to a well-defined outcome.
   • Example: Tossing a coin or rolling a die.

2. Sample Space (S)

   • The set of all possible outcomes of an experiment.
   • Example: For a coin toss
     S={H,T}.
   • For rolling a six-sided die
     S={1,2,3,4,5,6}.

3. Event (E)

   • A subset of the sample space. It represents one or more outcomes of an experiment.
   • Example: Getting an even number on a die roll:
     E={2,4,6}.

4. Probability P(E)

   • A measure of how likely an event is to occur, ranging from 0 (impossible) to 1 (certain).
   • Formula:
     ​
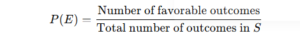
   • Example: For rolling a die, the probability of getting a 4:
     

Types of Probability

1. Classical Probability

   • Based on equally likely outcomes.
   • Example: The probability of drawing an Ace from a standard deck of 52 cards:
     ​

2. Empirical Probability

   • Based on observations or experiments.
   • Example: If a survey finds that 30% of people prefer a specific insurance plan, the empirical probability is P=0.3

3. Subjective Probability

   • Based on personal judgment or experience.
   • Example: An actuary may estimate a 70% chance of a flood in a region based on historical patterns and intuition.

Probability Rules

1. Addition Rule (For mutually exclusive events A and B):

   

   Example: For a die roll, the probability of getting a 2 or 4:

   
   

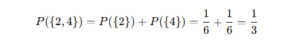
2. Multiplication Rule (For independent events A and B):
   

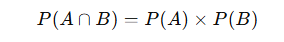
   Example: For two coin tosses, the probability of getting heads both times:

   ​

3. Complement Rule:

   

   Example: For rolling a die, the probability of NOT getting a 5:

   

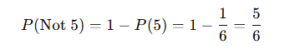
Conditional Probability

Conditional probability deals with the likelihood of an event occurring, given that another event has occurred.

• Formula:
  ​
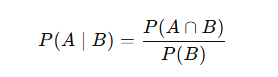
• Example: In a bag with 5 red and 3 blue balls, the probability of drawing a red ball given a red ball was already drawn (without replacement):

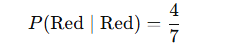
Applications in GIC Re

1. Risk Analysis

   • Evaluating the probability of natural disasters, market volatility, or claim frequency.
   • Example: Predicting the likelihood of a cyclone based on historical weather patterns.

2. Premium Calculation

   • Determining fair premiums based on the probability of events like accidents or health issues.

3. Reserve Estimation

   • Using probability to estimate future liabilities and maintain solvency.

4. Decision Making

   • Assessing the likelihood of events to guide underwriting, investments, and risk transfers.

Examples for Practice

1. A bag contains 3 red balls, 4 green balls, and 5 blue balls. What is the probability of randomly selecting a green ball?
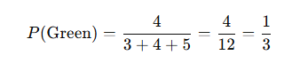
2. In a health insurance portfolio, the probability of an individual filing a claim is 0.2. If the portfolio contains 500 individuals, what is the expected number of claims?

Conclusion

Understanding the basics of probability theory lays the foundation for complex actuarial models. By mastering these principles, GIC Re actuaries can evaluate risks, predict uncertainties, and make data-driven decisions, ultimately contributing to the company’s resilience and profitability.